Data Analysis for Investment & Control
Quantative Analysis #02 - 주가와 거래량 필터링: MA, EWMA 본문
Moving Average
주가나 거래량에 대한 일별 데이터는 중장기적으로 시간 프레임을 잡고 분석하기에 굉장히 들쭉날쭉하다.
따라서, 신호를 적절히 가공시켜줄 필요가 있는데, 주가 차트에서도 많이 사용하는 이동평균선과 같은 것들이 그것이다. 일반적으로 5일, 20일, 60일 등에 대한 이동평균선을 많이 사용하는데, 일주일, 한달, 1분기에 대한 주가의 평균이라고 보면 된다. 일일 주가도 자세히 보면 초단위, 분단위로 움직임이 있지만 이렇게 빠른 시간 안에 매매를 수행하는 스캘퍼(Scalper)들이나 데이트레이딩을 하는 사람이 아니고서는 세밀하게 볼 필요는 없다.
신호처리에 있어서 가장 단순한 형태의 필터는 Moving Average 일 것이다. 간단하게도 양수 N개 만큼의 과거 값의 평균을 구하는 것이다.
지난 시간에 사용했던 삼성전자의 60일치 주가/거래량 데이터를 가지고 이동평균(Moving Avarage)을 적용해보자.
60일치의 데이터 밖에 없으므로 60개에 대한 이동평균은 의미가 없다!!
확실이 Raw Signal에 비해 5일/20일에 대한 이동평균선이 들쭉날쭉 한것이 없어진 것을 볼 수 있다. 어떻게 보면 신호를 뭉개뜨리기 때문에 고유의 특징을 없애는 것일 수도 있으므로 적당한 크기의 이동평균을 구해 사용하는 것이 중요하다.
고주파 성분을 없애는 효과를 가지고 있다는 면에서 Low Pass 필터와 유사한 점이 있다.
Exponential Weighted Moving Average, EWMA
이름이 참 길다..ㅋㅋㅋ
직역하자면, 지수 가중 이동 평균이라고 부른다.
수식의 유도는 어떻게 도출했는지는 모르나, 긴 이름에 비해서 수식은 오히려 이동평균 보다도 간단하다.
필터 출력을 y, 입력을 x라고 하고, k번째 대한 신호에 대한 수식은 다음과 같다.
여기서 α는 최근 데이터의 반영율을 의미한다. 값은 0 ≤ α ≤ 1의 범위를 갖는다. 순차적으로 생각해 볼 때, 이전(k-1) 의 값은 이미 계산되어 있는 값이므로 두 번의 곱셈과 한 번의 덧셈으로 계산이 끝난다는 것을 알 수 있다. 이동 평균의 계산식이 N의 크기가 커질 수록 연산량도 많아지는 것에 비해 간단하다고 할 수 있겠다.
EWMA 필터를 삼성전자 주가 신호에 적용시켜 보도록 하자.
파란색이 실제 주가 데이터이고, 녹색과 빨간색이 EWMA 필터가 적용된 형태이다. α값에 따라서 최근 경향의 반영 비중이 조정되는 것을 알 수 있다. α이 1이면 필터 효과가 전혀 없다. 수식적으로도 y(k) = x(k)가 된다.
이와는 다르게 이동평균선에서는 최근 경향에 대한 비중 조정이나 그런 것은 적용되지 않는다. 과거 N개의 값이 동일한 비중으로 적용되기 때문이다.
따라서, 신호의 최근 경향성을 좀 더 반영하고 싶다라면 EWMA 필터를 사용하여 적절한 값의 α값을 선택해 주면 된다.
거래량 미분, 필터링...
거래량은 주식 매매에 참여한 사람의 수와 비례하기 때문에 관심도를 대변하는 지표이다. 어쩌면 거래량의 변화를 감지함으로써 주가 움직임의 방향을 예측할 단서로 사용할 수도 있다.
수학시간에 배워서 알고 있듯이 어떤 함수 y = f(x)가 있을 때, 이 함수의 미분 f'(x)가 0인 지점은 함수의 값이 상승했다가 하락하거나 하락했다가 다시 상승하는 지점을 의미한다. 그러므로 거래량 신호의 미분값이 0인 지점은 거래량이 감소했다가 증가하거나 증가했다가 감소하기 시작하는 지점인 것이다.
주식 차트에 있어서 갑자기 거래량이 폭발적으로 증가한다거나 반대의 경우에는 주식의 가격이 상승 국면이나 하락 국면으로 진입하게 될 가능성이 높다.
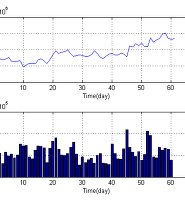
하단의 그래프는 원래 거래량을 나타내고 위의 그래프는 거래량의 미분과 미분 데이터를 EWMA 필터(α=0.3)로 필터링 한 결과이다. 원본 신호가 움직임이 다양하게 나타나기 때문에 미분한 신호에서도 smooth 함이 덜한 것을 볼 수 있다. EWMA 필터를 적용하여 좀 더 신호가 smooth 해 지도록 해 보았다.
이 문서를 포스팅하면서 샘플로 사용한 삼성전자 주가에서는 거래량 미분과 주가의 움직임과의 상관 관계가 뚜렷하게 나타나지는 않았다. 그리 간단하게 의미있는 결과가 나올 거라는 것도 욕심이긴 하다. 하지만 조금 더 연구를 진행해 보면 뭔가 의미있는 결과를 발견하지 않을까.
'Investment > 계량분석' 카테고리의 다른 글
| 마법공식 파헤치기 (4) | 2016.11.03 |
|---|---|
| Quantative Analysis #05 - 기본적인 주가지표를 통한 스크리닝 (0) | 2016.08.16 |
| Quantative Analysis #04 - 거시경제 지표의 사용 (1) - 도입 (1) | 2015.04.26 |
| Quantative Analysis #03 - 기술적 지표의 의미와 공식 (1) | 2015.03.31 |
| Quantative Analysis #01 - 삼성전자 주가 신호 분석 (0) | 2015.03.25 |